Atualmente estou estudando Clojure e agora quase finalizando o sementre da universidade estão surgindo os trabalhos de implementação e resolvi fazê-los usando Clojure, por que não uma boa nota e a aprovação na disciplina para dar uma motivada não é não? 8D, e pretendo descrever alguns por aqui até para deixar meio documentado também, então vamos lá.

Search A*
O algoritmo A* (A estrela), é um algoritmo de busca, de caminho em grafo, heurística, algoritmos de busca heurística utilizam informações extras sobre o domínio problema para guiar o processo de busca.
http://maratonapuc.wikidot.com/apostilas:a-star
http://www.dainf.ct.utfpr.edu.br/~fabro/IA_I/busca/IA_Estrategias_Busca_Inf.pdf
http://www.cos.ufrj.br/~ines/courses/cos740/leila/cos740/apres_ia.pdf
https://pt.wikipedia.org/wiki/Algoritmo_A*
Função Heurística (h(n))
Utilizando uma função estima-se o custo de um determinado nó(estado) até o objetivo final para ver o quanto esse estado é bom o suficiente para atingir o objetivo em relação aos outros estados, essa função é conhecida como função heurística (h). Essa função é específica para cada problema e deve ser analisada e criada de acordo com o mesmo.
Função de custo (g(n))
Usando outra função (g), avalia-se o custo total para chagar do estado inicial até o estado que esta sendo avaliado.
Função de avaliação (f(n))
A função global de avaliação (f(n)) dá-se pela soma da função heurística h(n) e a função de custo g(n), f(n) = g(n) + h(n).
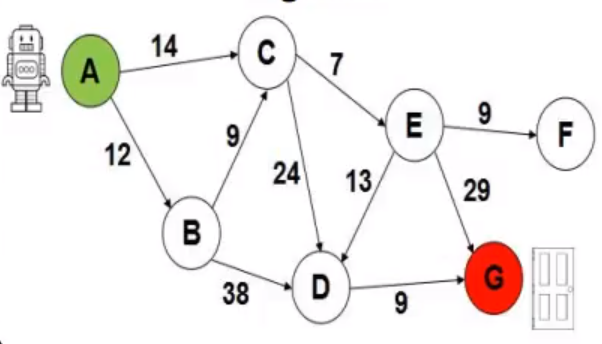
Para esse exercício utilizei um grafo como na imagem a seguir, o objetivo
é ir do estado A até o estado G pelo menor caminho.
Criando o projeto
Caso não saiba como criar um projeto em clojure, tem um artigo com uma
introdução para criação projetos e dependências em Clojure:
Vou criar um projeto chamado astar-algorithm-clojure utilizando o
Liningen:
lein new astar-algorithm-clojure
Após isso, teremos a estrutura de dirétório do projeto, irei criar todas
as funções no arquivo padrão core.clj no diretório src.

Usando Map criei a estrutura que irá representar o grafo da
imagem, onde temos os estados pais e os estados filhos com o valor de
custo para ir do estado pai até o respectivo estado filho.
Onde :A é o estado pai e :C e :B são seus estado filhos,
14 e 12 são os custos para ir de :A até os estados filhos
respectivos e assim é com os outros estados também.
Utilizarei valores já processados para a função heurística de cada estado, também usando Map para representar essa função.
Nesse exemplo, aplicando a função heurística para o estado :A retorna
o valor 30, para :B retorna 26. Esse é o valor heurístico
dos estados, que será somado ao custo do estado para calcular o custo
total do caminho por esse estado.
Pode-se usar diversas formas para essa
função heurística, como por exemplo Manhattan Distance, e
Euclidean Distance.
Vamos criar duas funções, state-children e children-values onde
state-children recebe um estado e retorna seus estados filhos em uma lista
e children-values recebe um estado e retorna o custo associado aos
estados filhos.
Passando o estado :A para a função state-children retorna o seus
estado filhos (:C :B) e para a função children-values retorna o
custo associado aos seus filhos (14 12).
Agora criaremos nossas funções de custo (g) e heurística (h), a função
h recebe um estado e retorna seu valor heurístico, e a função g
recebe o custo total atual e o custo de um estado filho o qual se esta
avaliando, e retorna o somatório de ambos.
Para nosso exemplo com o estado :A passando para a função h
retornará o valor 30 e a função g, pegando como exemplo o estado
:B para avaliar e passando o custo total atual como 0 teremos
(0 + 12).
A nossa função de avaliação recebera o custo do estado que esta sendo
avaliado, o estado que esta sendo avaliado, e o custo total atual e irá
aplica a soma da função g e h.
A proxíma função get-costs é responsável por calcular o custo, usando
a função de avaliação, para ir a cada estado filho do estado atual,
retornando todos os custos em uma lista.
Tomando como custo total atual 10 e o estado atual :A, a função
retornará (54 52).
A função get-next-state recebe o estado atual e os custos de seus
estados filhos, e retorna o estado filho que teve o menor custo calculado
pela função get-costs, como teve o menor custo, esse estado será o
próximo do caminho.
A função get-real-cost soma o custo atual do caminho com o custo do
próximo estado retornado pela get-next-state, para ir guardando o custo
total do caminho.
E agora a função goal-test recebe um estado e apenas verifica se o
estado é o objetivo.
A função principal do algoritmo, search-A*, recebendo apenas um estado
como parâmetro, que será o estado inicial :A, irá realizar uma
chamada recursiva passando o estado, o custo total atual como 0, e um
vetor vazio onde irá guardar os estado que farão parte do caminho (linha 2).
Primeiro testa se o estado atual é o ojetivo (linha 4), se não for,
verifica se o estado possui estados filhos (linha 8), caso possui,
irá pegar o custo para ir para cada um dos estado filhos em uma lista
costs (linha 9), após isso, irá pegar o estado filho com menor
custo get-nest-state (linha 10).
Depois de descobrir o estado de menor custo, faz uma chamada recursiva
passando o estado retornado de menor custo, next-state, como estado
atual, o calculo do custo como custo total atual, e o vetor com o estado
inserido, para o próximo processamento (linha 11).
Executando essas ações recursivamente até encontrar o estado objetivo
(linha 4), ao encontrar o estado objetivo apenas vai inseri-lo no
vetor onde estão os estados do caminho, imprimir o caminho encontrado e
o custo total do caminho.
E a função inicial do algoritmo que vai chamar a search-A*
Se rodarmos o algoritmo com o exemplo feito, teremos a seguinte saida:
[:A :C :E :D :G]
43
Que é o caminho mais curto encontrado pelo algoritmo e o custo total do caminho.
Uma questão que ficou em aberto nesse exemplo é quando o algoritmo encontrar um estado sem filhos, simplesmente irá parar, uma solução pode ser implmentar uma forma de retroceder até um estado que tenha estados filhos para continuar o processo.
Conclusão
O objetivo é só demostrar uma alternativa de implementação e como resolvi os trabalhos em Clojure, além de praticar o desenvolvimento nessa tecnologia que estou estudando. Não entrei em detalhes sobre a linguagem, espero escrever mais sobre futuramente, também como irá surgir novos trabalhos do curso tentarei resolvê-los utilizando Clojure e se possível escrever algo sobre também como forma de estudar.
O código completo podem ver aqui
Dúvidas, sugestões… podem deixar comentários, e compartilhar caso gostou :D.





